Recently the Supreme Court heard oral argument in Benisek v. Lamone, the second partisan-gerrymandering case this term (Gill v. Whiftord was the first). Clearly the Court intends to act. But the Justices also seem to have run aground on some fairly central questions: settling on a legal theory and a manageable standard to define the violation. Is action on partisan gerrymandering doomed?
In a recent working paper, Brian Remlinger and I argue that all is not lost, once the mathematical tools offered to the Court are organized into a proper framework. Indeed, our proposed framework can help to define a manageable standard for partisan gerrymandering.
Examination of the cases at hand has revealed the need for a flexible doctrine. Benisek concerns a single Congressional district in Maryland, while the other case, Gill v. Whitford, concerns the entire State Assembly of Wisconsin. The plaintiffs offered differing legal theories: in Benisek, a theory based on viewpoint discrimination and the First Amendment; and in Whitford, a theory based on both the First Amendment and the Fourteenth Amendment and the principle of equal protection. Resolving these competing theories is the Court’s first challenge.
But then we get to the fact that the evidence is largely mathematical in nature. This is a stumbling block. It’s not only that judges may be allergic to math; it’s also the ever-multiplying metrics and formulas that the Justices likely find daunting. Proposed tests have included the mean-median difference, the drawing of hundreds or thousands of alternative maps, and the recently-invented efficiency gap. Chief Justice Roberts even referred to this last measure as “sociological gobbledygook.” And we haven’t even gotten to a third case waiting in the wings, Rucho v. Common Cause, which tests a congressional gerrymander in North Carolina. Rucho does an excellent job of using many mathematical tests – perhaps too many. Let us not even mention a recent Pennsylvania case, in which a probability theorem was used. To the Justices the whole thing might look like the crowded cabin scene in the Marx Brothers classic A Night At The Opera.
I don’t think the situation is all that dire. But what would really help is a conceptual framework. Think of these tests as tools – and a good craftsman needs more than one tool. The array of standards on display is an impressive but disorganized set of tools. With a good conceptual framework, these tests start to look more orderly – and may even comprise a toolkit to serve a coherent legal theory.
The core premise of our working paper is that the various mathematical tests of partisan gerrymandering can be sorted into two categories according to questions they can answer: (1) Does the targeted political party have an unequal opportunity to elect representatives in a given election? (2) Are the resulting outcomes inequitable in a durable manner? The first category draws on ideas borrowed from racial discrimination law, while the second category extends that doctrine in directions that are unique to the arena of partisanship.
Opportunity is easily defined and corresponds to a core principle of democracy: it should be possible to vote out a candidate or incumbent. Because voters are clustered into enclaves that sometimes make an incumbent or party safe, redistricters can manipulate lines to amplify the effects of that natural clustering. Just as members of a racial group can have its representational rights impaired through gerrymandering, so it is with partisans.
Where partisans of the disfavored party comprise close to half the voters of a state (as in Whitford or Rucho), a statewide evaluation is the best approach. In contrast, many of the statewide tests are inappropriate when partisans of the disfavored party comprise a small fraction of the population (as in Benisek). In these cases, a better procedure is to examine individual districts. In this situation, tests of unequal opportunity are easily conceptualized as an extension of racial discrimination against minority voters. These contrasting situations – opposing party as equal opponent and opposing party as targeted minority – require different approaches.
However, party is a more mutable characteristic than race. This brings us to the second category: testing whether a partisan advantage is durable and resistant to change of voter preferences. Our second category, testing for inequality of outcome, addresses this problem by probing whether a particular arrangement is likely to withstand ordinary changes in voter sentiment that may occur over the course of a redistricting cycle. Such changes can be gauged not just by waiting for multiple elections to pass (which would vitiate the remedy) but by examining likely outcomes under a variety of possible electoral conditions. This is well within the reach of modern expert witnesses.
In short, opportunity tests evaluate whether or not a gerrymander has handicapped a party in a particular election by tilting the playing field, while outcome tests measure the size of the resulting representational advantage. An effective gerrymander achieves a distorted outcome by limiting opportunity. Therefore courts can use these two types of test to systematically investigate whether an offense has been committed and should be remedied.
How much partisanship is too much?
Once we’ve understood that tests for gerrymandering come in two varieties (outcome tests and opportunity tests), the next question is how to determine when a partisan gerrymander is excessive. Eventually, the Supreme Court (or lower courts) will have to decide how much partisanship is too much. But as Justice Kennedy wrote in his concurrence in Vieth v. Jubelirer, “[e]xcessiveness is not easily determined.” Here, longstanding traditions in the sciences can help.
In tests of unequal opportunity, a baseline for comparison is what would occur under districting processes in which partisan interests are not the overriding consideration. This involves significance testing, in which a district or statewide districting scheme can be reliably identified as more extreme than the great majority of possibilities that could arise incidentally through a districting process driven by criteria other than extreme partisanship.
Statistical measures of partisanship do not become tests until a bright-line threshold is drawn. When the measurement returned is beyond the threshold, the alarm is sounded. Statisticians, like judges, necessarily must settle on tests that remove reasonable doubt. In the field of statistical science, the process of choosing the correct threshold for a test is known as sensitivity testing. In voting rights, the Court has sometimes engaged in threshold setting. For example, the one person, one vote principle has led to a requirement that congressional districts be of perfectly equal population to within one person. With partisan-gerrymandering law in its infancy, sensitivity testing may help lower courts set useful thresholds for the many tests of opportunity.
One possible threshold might be that a test of opportunity should flag states where the probability is less than 1 in 20 that a plan arose by incidental means. This is called the “p<0.05 standard” in the sciences, reflecting a determination of statistical significance. Once statistical significance is found, then measures of outcome can give a sense of the size of an effect. An inequitable outcome might be defined as a distortion of at least one seat. In states which had single-party control of redistricting in the post-2010 cycle, these criteria (one seat and p<0.05) would have identified seven state congressional maps as extreme partisan gerrymanders.
A two-part framework for identifying an extreme partisan gerrymander
With the categories of unequal opportunity and inequitable outcome in hand, it is possible to sort out the mathematical tools into these two bins. It is further possible to sort the tools according to specific situations having to do with the number of districts in a state and the degree to which the targeted party is in a minority. By spelling out which tests are applicable in a particular circumstance, our working paper helps courts best address whatever cases they may encounter.
A court deciding whether a partisan gerrymander is unconstitutional could then apply a two-part test: (1) Does the map unduly deny one party an equal electoral opportunity? (2) Is the resulting outcome advantage substantial, and resistant to changes in voter sentiment? Each of these questions can be answered with the aid of various math tools—which our cheat sheet (from our working paper) helpfully organizes below. If the answer to both questions is “Yes” then the map fails the test and the partisan gerrymander is unconstitutional.
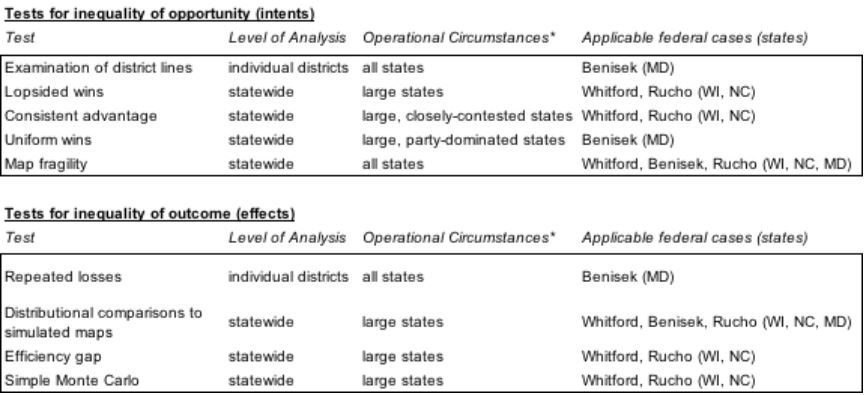
Our two-part classification is conceptually not far from the original formulation of the 1986 landmark case of Davis v. Bandemer, which first made partisanship in redistricting a justiciable Equal Protection violation. There, Justice Byron White wrote (for a plurality of the Court) that plaintiffs must prove both discriminatory intent and discriminatory effect. If we construe inequality of opportunity as an indication of the redistricters’ likely intent, and a persistent inequitable outcome as the effect of the gerrymander, then the framework that Brian and I propose neatly aligns with the Justices’ first crack at tackling partisan gerrymandering over thirty years ago – but this time with a practical solution.